Which Trigonometric Functions Have A Defined Amplitude? (Select All That Apply.)

Trigonometric Functions

Trigonometric functions are the basic six functions that have a domain input value as an angle of a right triangle, and a numeric answer as the range. The trigonometric function of f(x) = sinθ has a domain, which is the angle θ given in degrees or radians, and a range of [-1, 1]. Similarly we have the domain and range from all other functions. Trigonometric functions are extensively used in calculus, geometry, algebra.

Here in the below content, we shall aim at understanding the trigonometric functions across the four quadrants, their graphs, the domain and range, the formulas, and the differentiation, integration of trigonometric functions

1.	What Are Trigonometric Functions?
2.	Principal Values of Trigonometric Functions
3.	Trigonometric Functions in Four Quadrants
4.	Solved Examples
5.	Practice Questions
6.	FAQs on Trigonometric Functions

What are Trigonometric Functions?

There are six basic trigonometric functions used in Trigonometry. These functions are trigonometric ratios. The six basic trigonometric functions are sine, cosine, secant, co-secant, tangent, and co-tangent. The trigonometric functions and identities are the ratio of sides of a right-angled triangle. The sides of a right triangle are the perpendicular side, hypotenuse, and base, which are used to calculate the sine, cosine, tangent, secant, cosecant, and cotangent values using trigonometric formulas. The formulas to find the trigonometric functions are as follows:

Trigonometric Formula

1. Basic Formulas

sin θ = Perpendicular/Hypotenuse
cos θ = Base/Hypotenuse
tan θ = Perpendicular/Base
sec θ = Hypotenuse/Base
cosec θ = Hypotenuse/Perpendicular
cot θ = Base/Perpendicular

Principal Values of Trigonometric Functions

The trigonometric functions have a domain θ, which is in degrees or radians. Some of the principal values of θ for the different trigonometric functions are presented below in a table. These principal values are also referred as standard values and are frequently used in calculations. The principal values of trigonometric functions have been derived from a unit circle. These values also satisfy all the trigonometric formulas.

Principal Values of Trigonometric Functions

Trigonometric Functions in Four Quadrants

The angle θ is an acute angle (θ < 90) and is measured with reference to the positive x-axis, in the anticlockwise direction. Further, these trigonometric ratios have different numeric signs (+ or -) in the different quadrants, which are based on the positive or negative axis of the quadrant. The trigonometric ratios of Sinθ, Cosecθ are positive in quadrants I and II, and are negative in quadrants III and IV. All the trigonometric functions have a positive range in the first quadrant. The trigonometric functions Tanθ, Cotθ are positive only in Quadrants I and III, and the trigonometric ratios of Cosθ, Secθ are positive only in quadrants I and IV respectively.

Trigonometric Functions in Four Quadrants

The trigonometric functions have values of θ, (90° - θ) in the first quadrant. The cofunction identities provide the interrelationship between the different complementary trigonometric functions for the angle (90° - θ).

sin(90°−θ) = cos θ
cos(90°−θ) = sin θ
tan(90°−θ) = cot θ
cot(90°−θ) = tan θ
sec(90°−θ) = cosec θ
cosec(90°−θ) = sec θ

The domain θ value for different trigonometric function in the second quadrant is (π/2 + θ, π - θ), in the third quadrant is (π + θ, 3π/2 - θ), and in the fourth quadrant is (3π/2 + θ, 2π - θ). For π/2, 3π/2 the trigonometric values changes as their complementary ratios such as Sinθ⇔Cosθ, Tanθ⇔Cotθ, Secθ⇔Cosecθ. For π, 2π the trigonometric values remain the same. The changing trigonometric ratios in different quadrants and angles can be understood from th below table.

Trigonometric Ratio	I - Quadrant	II - Quadrant		III-Quadrant		IV-Quadrant
	π/2 - θ	π/2 + θ	π - θ	π + θ	3π/2 - θ	3π/2 + θ	2π - θ
Sinθ	Cosθ	Cosθ	Sinθ	-Sinθ	-Cosθ	-Cosθ	-Sinθ
Cosθ	Sinθ	-Sinθ	-Cosθ	-Cosθ	-Sinθ	Sinθ	Cosθ
Tanθ	Cotθ	-Cotθ	-Tanθ	Tanθ	Cotθ	-Cotθ	-Tanθ
Cotθ	Tanθ	-Tanθ	-Cotθ	Cotθ	Tanθ	-Tanθ	-Cotθ
Secθ	Cosecθ	-Cosecθ	-Secθ	-Secθ	-Cosecθ	Cosecθ	Secθ
Cosecθ	Secθ	Secθ	Cosecθ	-Cosecθ	-Secθ	-Secθ	-Cosecθ

Graphing Trigonometric Functions

The graphs of trigonometric functions have the domain value of θ represented on the horizontal x-axis and the range value represented along the vertical y-axis. The graph of Sinθ and Tanθ passes through the origin and the graphs of other trigonometric functions do not pass through the origin. The range of Sinθ and Cosθ is limited to [-1, 1]. The range of infinite values is presented as drawn beside the dotted lines.

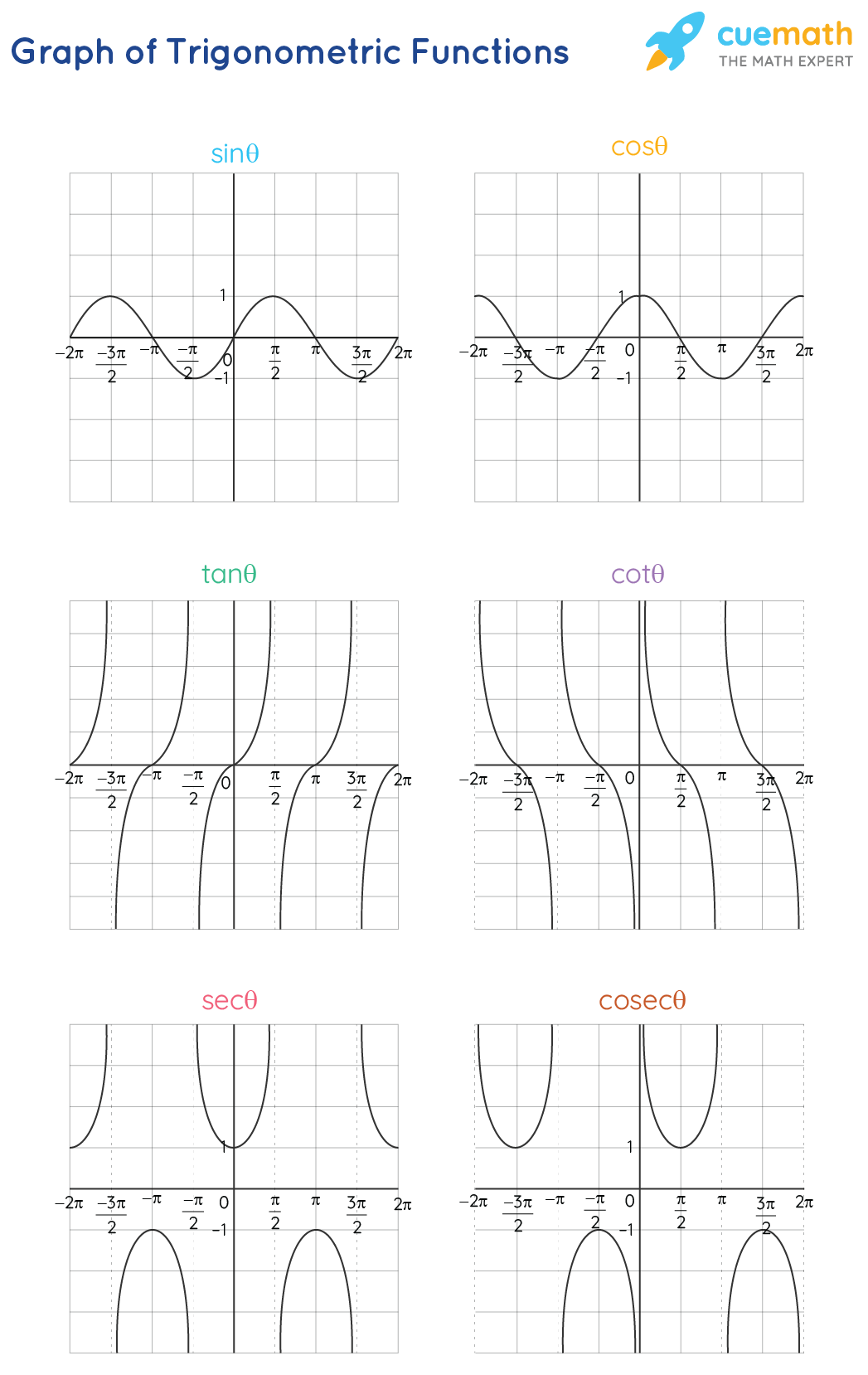
Graph of Trigonometric Functions

Domain and Range of Trigonometric Functions

The value of θ represents the domain of the trigonometric functions and the resultant value is the range of the trigonometric function. The domain values of θ are in degrees or radians and the range is a real number value. Generally, the domain of the trigonometric function is a real number value, but in certain cases, a few angle values are excluded because it results in a range as an infinite value. The below table presents the domain and range of the six trigonometric functions.

Trigonometric Functions	Domain	Range
Sinθ	(-∞, + ∞)	[-1, +1]
Cosθ	(-∞ +∞)	[-1, +1]
Tanθ	R - (2n + 1)π/2	(-∞, +∞)
Cotθ	R - nπ	(-∞, +∞)
Secθ	R - (2n + 1)π/2	(-∞, -1] U [+1, +∞)
Cosecθ	R - nπ	(-∞, -1] U [+1, +∞)

Trigonometric Function Formulas

The trigonometric functions formulas are broadly divided into reciprocal identities, Pythagorean formulas, sum and difference of identities, formulas for multiple and sub-multiple angles, sum and product of identities. All of these below formulas can be easily derived using the ratio of sides of a right-angled triangle. The higher formulas can be derived by using the basic trigonometric function formulas. Reciprocal identities are used frequently to simplify trigonometric problems.

Reciprocal Identities

cosec θ = 1/sin θ
sec θ = 1/cos θ
cot θ = 1/tan θ
sin θ = 1/cosec θ
cos θ = 1/sec θ
tan θ = 1/cot θ

Pythagorean Identities

Sin²θ + Cos²θ = 1
1 + Tan²θ = Sec²θ
1 + Cot²θ = Cosec²θ

Sum and Difference Identities

sin(x+y) = sin(x)cos(y) + cos(x)sin(y)
cos(x+y) = cos(x)cos(y) – sin(x)sin(y)
tan(x+y) = (tan x + tan y)/ (1−tan x • tan y)
sin(x–y) = sin(x)cos(y) – cos(x)sin(y)
cos(x–y) = cos(x)cos(y) + sin(x)sin(y)
tan(x−y) = (tan x–tan y)/ (1+tan x • tan y)

Half-Angle Identities

\(\begin{array}{l}
\text { - } \sin \frac{x}{2}=\pm \sqrt{\frac{1-\cos x}{2}} \\
\text { - } \cos \frac{x}{2}=\pm \sqrt{\frac{1+\cos x}{2}} \\
\text { - } \tan \left(\frac{x}{2}\right)=\sqrt{\frac{1-\cos (x)}{1+\cos (x)}} \\
\text { Also, } \tan \left(\frac{x}{2}\right)=\sqrt{\frac{1-\cos (x)}{1+\cos (x)}} \text { So, } \tan \left(\frac{x}{2}\right)=\frac{1-\cos (x)}{\sin (x)} \\
=\sqrt{\frac{(1-\cos (x))(1-\cos (x))}{(1+\cos (x))(1-\cos (x))}} \\
=\sqrt{\frac{(1-\cos (x))^{2}}{1-\cos ^{2}(x)}} \\
=\sqrt{\frac{(1-\cos (x))^{2}}{\sin ^{2}(x)}} \\
=\frac{1-\cos (x)}{\sin (x)}
\end{array}\)

Double Angle Identities

sin(2x) = 2sin(x) • cos(x) = [2tan x/(1+tan² x)]
cos(2x) = cos²(x)–sin²(x) = [(1-tan² x)/(1+tan² x)]
cos(2x) = 2cos²(x)−1 = 1–2sin²(x)
tan(2x) = [2tan(x)]/ [1−tan²(x)]
cot(2x) = [cot²(x) - 1]/[2cot(x)]
sec (2x) = sec²x/(2-sec² x)
cosec (2x) = (sec x. cosec x)/2

Triple Angle Identities

Sin 3x = 3sin x – 4sin³x
Cos 3x = 4cos³x-3cos x
Tan 3x = [3tanx-tan³x]/[1-3tan²x]

Product identities

2sinx⋅cosy=sin(x+y)+sin(x−y)
2cosx⋅cosy=cos(x+y)+cos(x−y)
2sinx⋅siny=cos(x−y)−cos(x+y)

Sum of Identities

sinx+siny=2sin((x+y)/2) . cos((x−y)/2)
sinx−siny=2cos((x+y)/2) . sin((x−y)/2)
cosx+cosy=2cos((x+y)/2) . cos((x−y)/2)
cosx−cosy=−2sin((x+y)/2 . sin((x−y)/2)

Inverse Trigonometric Functions

Inverse trigonometric functions are the inverse ratio of the basic trigonometric ratios. Here the basic trigonometric function of Sin θ = x, can be changed to Sin^-1 x = θ. Here x can have values in whole numbers, decimals, fractions, or exponents. For θ = 30° we have θ = Sin^-1 (1/2). All the trigonometric formulas can be transformed into inverse trigonometric function formulas.

Inverse Trigonometric Function

Arbitrary Values: The inverse trigonometric ratio formula for arbitrary values is applicable for all the six trigonometric functions. For the inverse trigonometric functions of sine, tangent, cosecant, the negative of the values are translated as the negatives of the function. And for functions of cosecant, secant, cotangent, the negatives of the domain are translated as the subtraction of the function from the π value.

Sin^-1(-x) = -Sin^-1x
Tan^-1(-x) = -Tan^-1x
Cosec^-1(-x) = -Cosec^-1x
Cos^-1(-x) = π - Cos^-1x
Sec^-1(-x) = π - Sec^-1x
Cot^-1(-x) = π - Cot^-1x

The inverse trigonometric functions of reciprocal and complementary functions are similar to the basic trigonometric functions. The reciprocal relationship of the basic trigonometric functions, sine-cosecant, cos-secant, tangent-cotangent, can be interpreted for the inverse trigonometric functions. Also the complementary functions, since-cosine, tangent-cotangent, and secant-cosecant can be interpreted into:

Reciprocal Functions: The inverse trigonometric formula of inverse sine, inverse cosine, and inverse tangent can also be expressed in the following forms.

Sin^-1x = Cosec^-11/x
Cos^-1x = Sec^-11/x
Tan^-1x = Cot^-11/x

Complementary Functions: The complementary functions of sine-cosine, tangent-cotangent, secant-cosecant, sum up to π/2.

Sin^-1x + Cos^-1x = π/2
Tan^-1x+ Cot^-1x = π/2
Sec^-1x + Cosec^-1x = π/2

Differentiation of Trigonometric Functions

The differentiation of trigonometric functions gives the slope of the tangent of the curve. The differentiation of Sinx is Cosx and here on applying the x value in degrees for Cosx we can obtain the slope of the tangent of the curve of Sinx at a particular point. The formulas of differentiations of trigonometric functions are useful to find the equation of a tangent, normal, to find the errors in calculations.

d/dx. Sinx = Cosx
d/dx. Cosx = -Sinx
d/dx. Tanx = Sec²x
d/dx. Cotx = -Cosec²x
d/dx.Secx = Secx.Tanx
d/dx. Cosecx = - Cosecx.Cotx

Integration of Trigonometric Function

The integration of trigonometric functions is helpful to find the area under the graph of the trigonometric function. Generally, the area under the graph of the trigonometric function can be calculated with reference to any of the axis lines and within a defined limit value. The integration of trigonometric functions is helpful to generally find the area of irregular shaped plane surfaces.

\(\int Sinx.dx= -Cosx + C\)
\(\int Cosx.dx= Sinx + C\)
\(\int Sec^2x.dx= Tanx + C\)
\(\int Cosec^2x.dx= -Cotx + C\)
\(\int Secx.Tanx.dx= Secx + C\)
\(\int Cosecx.Cotx.dx= -Cosecx + C\)
\(\int tanx.dx = log|secx| + c\)
\(\int cotx.dx = log|sinx| + c\)
\(\int secx.dx = log|secx + tanx| + c\)
\(\int cosecx.dx = log|cosecx - cotx| + c\)

Related Topics

The following related links help in understanding more about trigonometric identities.

Trigonometry
Trigonometry Formulas
Trigonometric Identities
Coordinate Geometry
Algebraic Identities

Example 1: Find the value of Sin75°.

Solution:

The aim is to find the value of Sin75°.

Her we can use the formula Sin(A + B) = SinA.CosB + CosA.SinB.

Here we have A = 30° and B = 75°

Sin 75° = Sin(30° + 45°)

= Sin30°.Cos45° + Cos30°.Sin45°

= \( \frac{1}{2}.\frac{1}{\sqrt2} + \frac{\sqrt3}{2}.\frac{1}{\sqrt2}\)

= \( \frac{\sqrt3 +1}{2\sqrt2}\)

Answer: Sin75° = \( \dfrac{\sqrt3 +1}{2\sqrt2}\)
Example 2: Find the value of the trigonometric functions, for the given value of 12Tanθ = 5.

Solution:

Given 12Tanθ = 5, and we have Tanθ = 5/12

Tanθ = Perpendicular/Base = 5/12

Applying the Pythagorean theorem we have:

Hypotenuse² = Perpendicular² + Base²

Hyp² = 12² + 5²

= 144 + 25

= 169

Hyp = 13

Hence the other trigonometric functions are as follows.

Sinθ = Adj/Hyp = 5/13

Cosθ = Base/Hyp = 12/13

Cotθ = Base/Adj = 12/5

Secθ = Hyp/Base = 13/12

Cosecθ = Hyp/Adj = 13/5

go to slidego to slide

Great learning in high school using simple cues

Indulging in rote learning, you are likely to forget concepts. With Cuemath, you will learn visually and be surprised by the outcomes.

Book a Free Trial Class

FAQs on Trigonometric Functions

What are the Six Trigonometric Functions?

The trigonometric functions are the result of the ratio of the sides of the right angles triangle. For the three sides of the triangle as hypotenuse, base, altitude, and for the angle between the hypotenuse and the base being θ, the value of the six trigonometric ratios are as follows.

Sinθ = Altitude/Hypotenuse
Cosθ = Base/Hypotenuse
Tanθ = Altitude/Base
Cotθ = Base/Altitude
Secθ = Hypotenuse/Base
Cosecθ = Hypotenuse/Altitude

How Do you Find Trigonometric Functions?

The trigonometric functions are the ratio of the sides of a right-angled triangle. Further, we also apply the Pythagorean rule of Hypotenuse² = Altitude² + Base². Also, the trigonometric functions have different values for different angle values between the hypotenuse and the base of the right triangle.

What is the Domain and Range of Trigonometric Functions?

The domain of a trigonometric function is the value of θ in Sinθ, and the range is the final numeric value of Sinθ. This concept can be similarly applied to all the other trigonometric functions. Further, the domain values can be any angular values, but here we have the principal values of angles as 0°, 30°, 45°, 60°, 90°. And the range is the highest and the lowest values which are obtained. It is [-1, 1] for sinθ, cosθ, and it is (-∞, +∞) for tanθ, cotθ.

What is the Result of Multiplying Six Trigonometric Functions?

The result of the multiplication of the six trigonometric functions is as follows. Sinθ.Cosθ.Tanθ.Cotθ.Secθ.Cosecθ = Sinθ.Cosθ.Sinθ/Cosθ.Cosθ/Sinθ.1/Cosθ.1/Sinθ = 1.

What is the General Solution of Trigonometric Function of Sinx?

The general solution of Sinx is nπ + (-1)ⁿx. This represents all the higher angle values of Sinx. For x = π/3 we have the higher values of x as 2π/3, 7π3, and the general solution of x is nπ +(-1)ⁿπ/3.

What is the General Solution of the Trigonometric Function of Cosx?

The general solution of Cosx is 2nπ + x. This general solution represents all the higher angle values of Cosx. For x = π/4, the higher values of x are 7π/4, 9π/4, and the general solution of x is 2nπ + π/4.

What is the General Solution of the Trigonometric Function of Tanx?

The general solution of Tanx is nπ + x. The general solution represents all the higher angle values of Tanx. For x = π/6, the higher values of x are 7π/6, 13π/6, and the general solution of x is nπ + π/6.

How to Differentiate Trigonometric Functions?

The differentiation of trigonometric function results in the slope of the tangent to the curve of the trigonometric function. The differentiation of sinx results in cosx, which by substituting the value of x in degrees gives the slope value of the tangent to the curve of sinx. The differentiation is calculated using the first principle of derivatives. Further, we have the differentiation of the six trigonometric functions as follows.

d/dx. Sinx = Cosx
d/dx. Cosx = -Sinx
d/dx. Tanx = Sec²x
d/dx. Cotx = -Cosec²x
d/dx.Secx = Secx.Tanx
d/dx. Cosecx = - Cosecx.Cotx

What are the Applications of Trigonometric Functions?

The trigonometric functions have numerous applications in calculus coordinate geometry algebra. The slope of a line, the normal form of the equation of a lie, parametric coordinates of a parabola, ellipse, hyperbola, are all calculated and represented using trigonometric functions. The trigonometric functions can be used to find the height of a tree, for the given distance of the tree from the point of observation. Further, the trigonometric functions are extensively used in astronomy, to find distances of stars and celestial bodies, with the help of the given angle value.